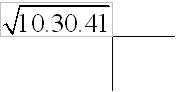SUMA Y RESTA DE ENTEROS
Si uno de los enteros es negativo, restar el valor absoluto de este al otro número. Ejemplo: 14 + (-6) = 14 – 6 = 8
Si los dos números enteros son negativos, suma su valor absoluto y coloca un signo negativo delante.
martes, 15 de noviembre de 2011
SIGNOS DE AGRUPACION
Al suprimir signos de agrupación, tenga en cuenta que si están precedidos de un menos, usted debe cambiar el signo de las cantidades encerradas dentro
MULTIPLICACION DE ENTEROS
Para multiplicar dos números enteros se multiplican sus valores absolutos; si los dos
factores tienen igual signo, el producto es positivo, y si los dos factores tienen
distinto signo, el producto es negativo
POTENCIAS DE ENTEROS
La potencia de exponente natural de un número entero es otro número entero, cuyo valor absoluto es el valor absoluto de la potencia y cuyo signo es el que se deduce de la aplicación
ECUACIONES DE ENTEROS
Es una igualdad entre dos expresiones
algebraicas, los cuales se denominan miembros de la ecuación. En ellas
aparecen números y letras (incógnita) relacionadas mediante una
operación matemática.
jueves, 28 de julio de 2011
Alturas, medianas, mediatrices y bisectrices de un triángulo
Altura es cada una de las rectas perpendiculares trazadas desde un vértice al lado opuesto (o su prolongación).
Ortocentro
Es el punto de corte de las tres alturas.
Medianas de un triángulo
Mediana es cada una de las rectas que une el punto medio de un lado con el vértice opuesto.
Baricentro
Es el punto de corte de las tres medianas.
El baricentro divide a cada mediana en dos segmentos, el segmento que une el baricentro con el vértice mide el doble que el segmento que une baricentro con el punto medio del lado opuesto.
BG = 2GA
Mediatrices de un triángulo
Mediatriz es cada una de las rectas perpendiculares trazadas a un lado por su punto medio.
Circuncentro
Es el punto de corte de las tres mediatrices.
Es el centro de una circunferencia circunscrita al triángulo.
Bisectrices de un triángulo
Bisectriz es cada una de las rectas que divide a un ángulo en dos ángulos iguales.
Incentro
Es el punto de corte de las tres bisetrices.
Es el centro de una circunferencia inscrita en el triángulo.
Recta de Euler
Angulos
Un ángulo es la parte del plano comprendida entre dos semirrectas que tienen el mismo punto de origen.[1] Suelen medirse en unidades tales como el radián, el grado sexagesimal o el grado centesimal.
Pueden estar definidos sobre superficies planas (trigonometría plana) o curvas (trigonometría esférica). Se denomina ángulo diedro al espacio comprendido entre dos semiplanos cuyo origen común es una recta. Un ángulo sólido es el que abarca un objeto visto desde un punto dado, midiendo su tamaño aparente.
Alturas de un triángulo
En un triángulo la altura respecto de un lado, es la distancia entre la recta que contiene al lado y el vértice opuesto. Equivale a un segmento perpendicular a dicho lado con un extremo en el vértice opuesto y el otro en dicho lado, o en su prolongación. La intersección de la altura y el lado opuesto se denomina «pie» de la altura.
La magnitud de la altura sirve para calcular el área de un triángulo, siendo su valor: a = b·h/2, donde a es el área, b la base –la longitud del lado "inferior"–, y h su altura correspondiente.
En la figura, pueden ser BC·AA"/2, AB·CC"/2 o AC·BB"/2.
Ésta fórmula se puede demostrar, geométricamente, trazando un rectángulo cuya área es el doble del área del triángulo, con la misma base y la misma altura.
jueves, 9 de junio de 2011
miércoles, 1 de junio de 2011
LOGARITMOS
El logaritmo de un número, en una base dada, es el exponente al cual se debe elevar la base para obtener el número.
Siendo a la base, x el número e y el logarítmo.
De la definición de logaritmo podemos deducir:
No existe el logaritmo de un número con base negativa.
No existe el logaritmo de un número negativo.
No existe el logaritmo de cero.
El logaritmo de 1 es cero.
El logaritmo en base a de a es uno.
El logaritmo en base a de una potencia en base a es igual al exponente.
Propiedades de los logaritmos:
1El logaritmo de un producto es igual a la suma de los logaritmos de los factores:
2 El logaritmo de un cociente es igual al logaritmo del dividendo menos el logaritmo del divisor:
3 El logaritmo de una potencia es igual al producto del exponente por el logaritmo de la base:
4El logaritmo de una raíz es igual al cociente entre el logaritmo del radicando y el índice de la raíz:
RAICES
La raíz cuadrada de un número no negativo es el que, multiplicado con sí mismo, nos da el número. Por si no has entendido gran cosa:
1.- La raíz cuadra de 
=
…... porque 
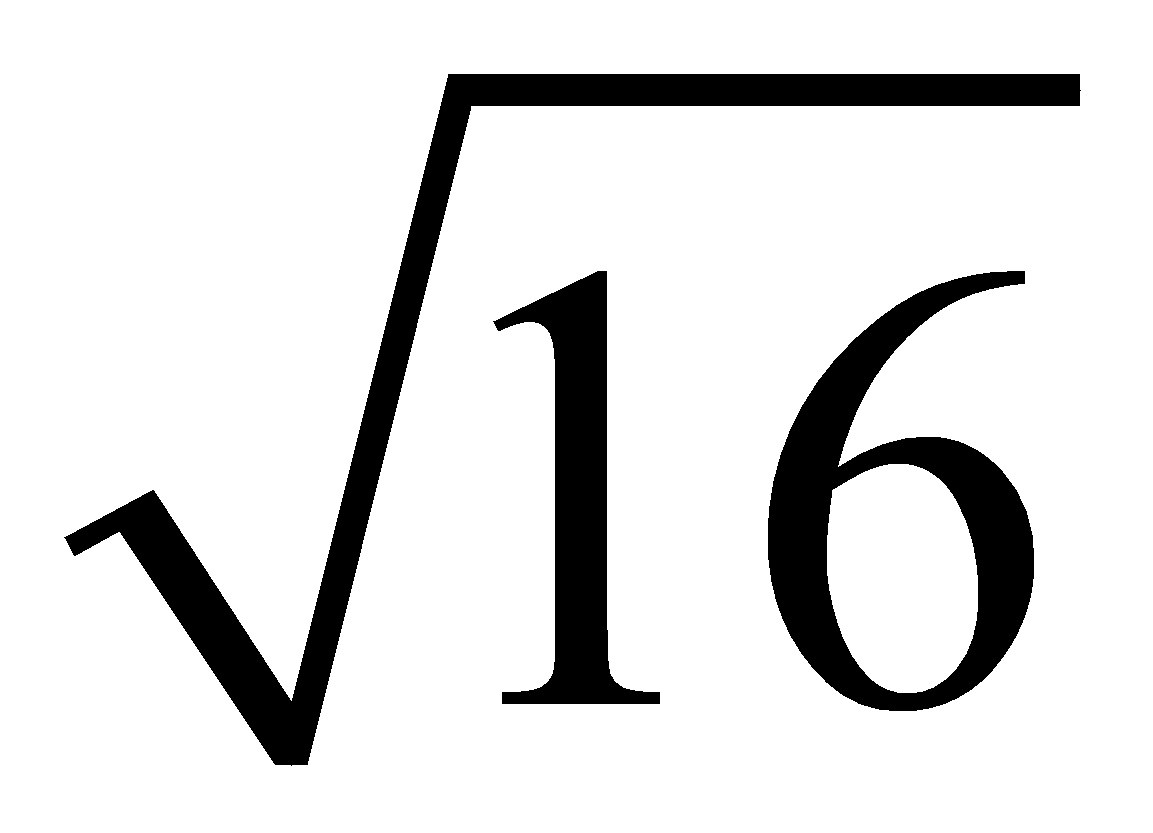
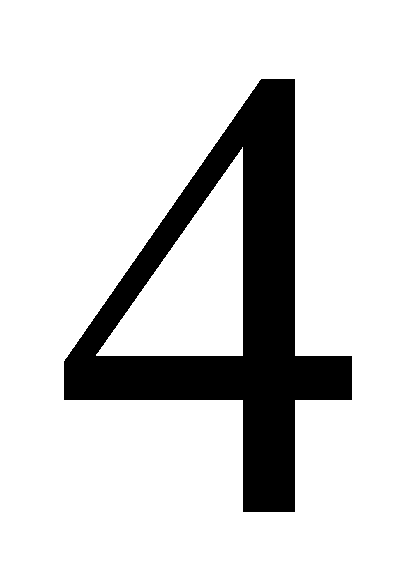
= …... porque 
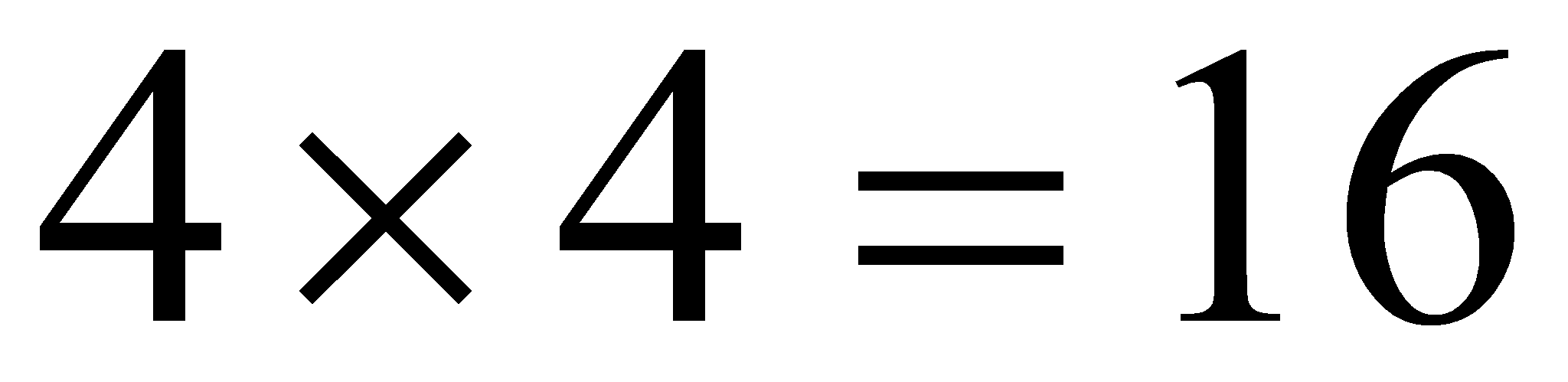
2.- No existen raíces cuadradas de números negativos.
RADICAL:
Se llama radical al signo 
que indica la operación para extraer raíces.
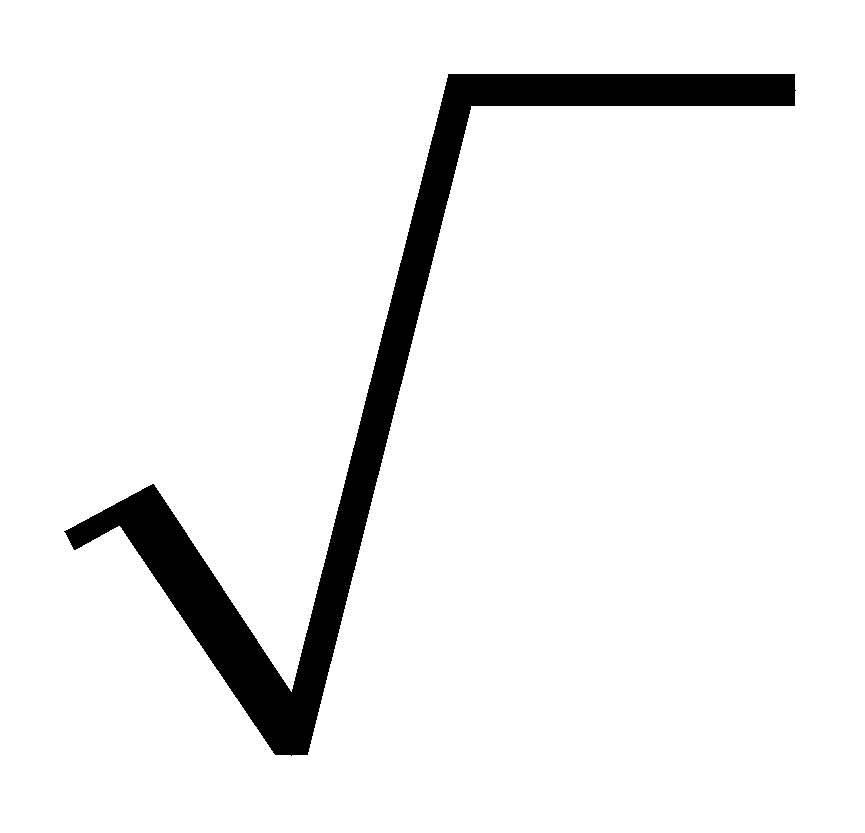
que indica la operación para extraer raíces.ÍNDICE:
Es el pequeño número que se coloca en el RADICAL:
En este caso hemos escrito un tres y se le llama raíz cúbica.
Si colocamos un 4 le llamaremos raíz cuarta:
En el caso de que no escribamos nada, se entiende que hay un 2 y su nombre es de raíz cuadrada:
RADICANDO:
La expresión que se encuentra debajo del signo radical se llama radicando:
El radicando es:1234
2.36 La raíz cuadrada tiene por objeto calcular un número de modo que si lo multiplicamos por sí mismo nos da el radicando: 
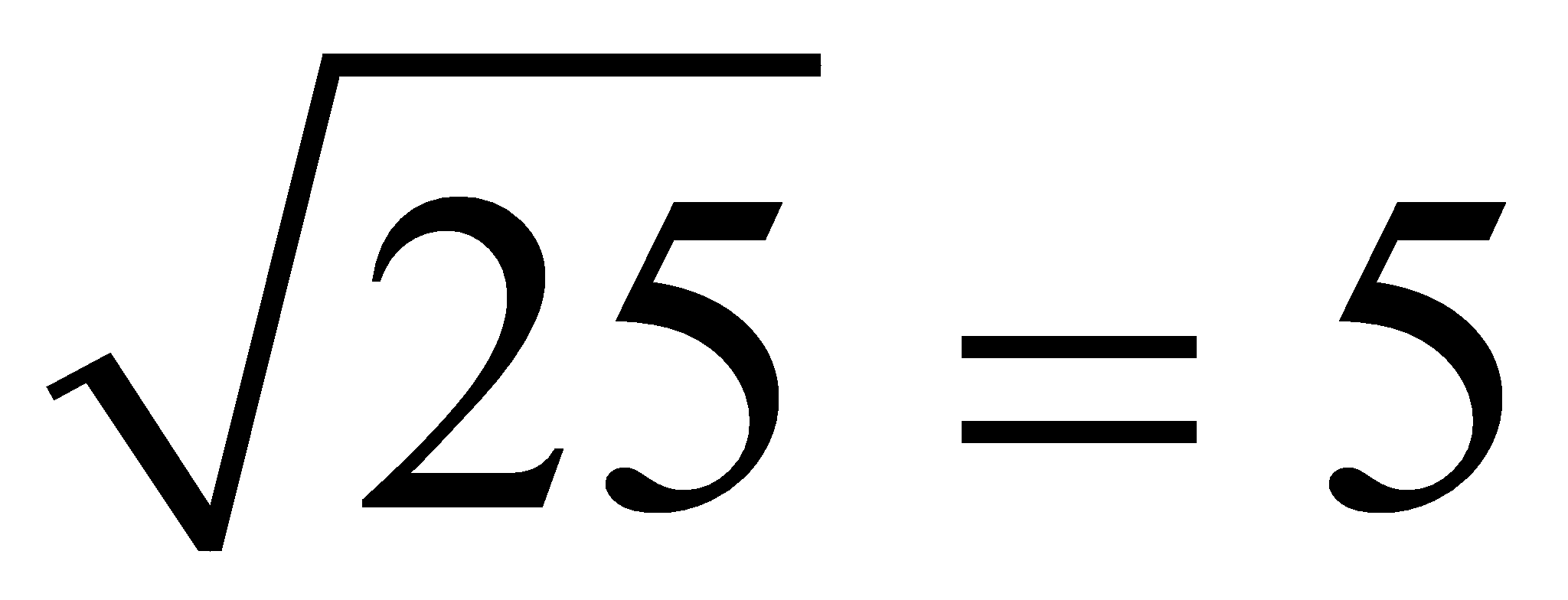
Significa que si multiplico 5 por sí mismo obtengo 25, es decir, la cantidad que está debajo del signo radical.
2.37 ¿Cuáles son las raíces cuadradas de:
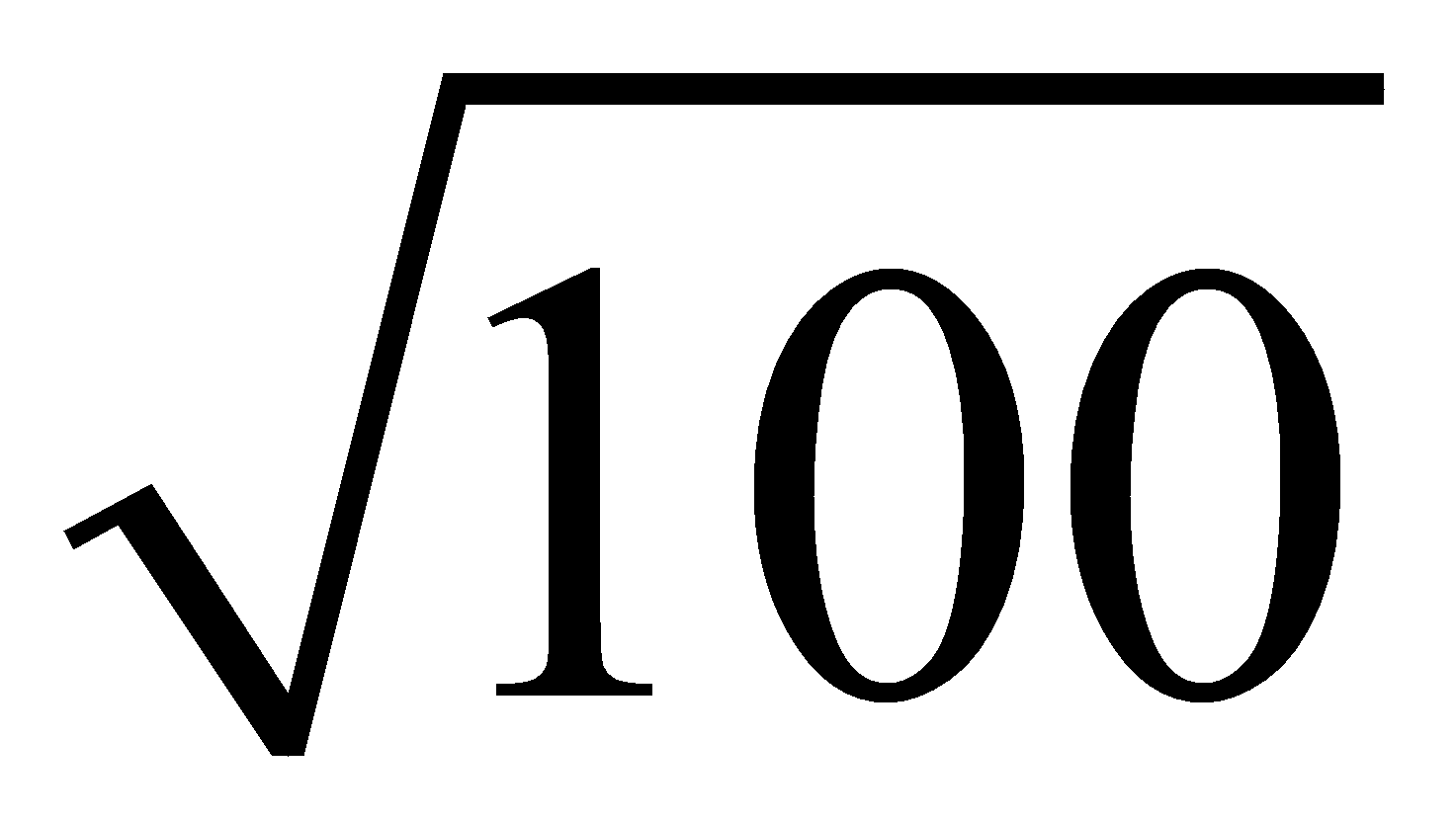
?Respuestas: 2, 3, 4, 8, 9 y 10.
CALCULAR LA RAÍZ CUADRADA DE UN NÚMERO GRANDE:
Se trata de una operación que se parece a una división, aunque un poco más difícil.
Imagina que queremos saber qué número elevado al cuadrado nos da 103041.
2.38 Vamos a hacer la raíz cuadrada de 103041 paso a paso:
Formamos grupos de dos cifras de derecha a izquierda.
El último grupo puede tener una cifra (porque no quedan más).
Trazamos las dos rectas que tienes a continuación:
Empezamos a trabajar de izquierda a derecha, buscamos un número que elevado al cuadrado nos de 10 o se acerque lo más posible a este valor. Se trata del 3, ya que 32 = 9.
jueves, 31 de marzo de 2011
Suscribirse a:
Entradas (Atom)